|
在已经测得平均客流量和平均服务时间的条件下,如何科学合理地确定营业员人数,并核定营业员的工作量和劳动报酬,便成为当前商业零售企业管理中迫切需要解决的问题,本文介绍了一个解决问题的数学方法
商业零售企业不同柜组之间由于客流量和服务时间的差异,各柜组所需营业员人数是不同的。营业员人数过少,顾客等待时间就长,会影响服务质量;营业员人数过多,则会造成人力资源的浪费,影响劳动效率。在已经测得平均客流量和平均服务时间的条件下,如何科学合理地确定营业员人数,并核定营业员的工作量和劳动报酬,便成为当前商业零售企业管理中迫切需要解决的问题。
设商业零售企业各服务系统(柜组)有m个营业员,当有顾客到来时,如有营业员空着,空着的营业员立即来服务,否则等着,直到有一个营业员接待完一个顾客后再来接待,顾客按先到先接受服务的原则进行排队,以N(t)表示时刻t正在接受和等待服务的顾客人数(顾客队伍长度,简称队长),当N(t)=i时,称“时刻t系统处于状态i”。
设一顾客已接受服务时间t,再接受服务时间△t与t无关,服务时间服从指数分布:
P{ξ≤t+△t|ξ>t}=1-P{ξ>t+△t|ξ>t}
=1-P{ξ>t+△t|ξ>t}/P{ξ>t}
=1-P{ξ>t+△t}/P{ξ>t}
商业零售企业不同柜组之间由于客流量和服务时间的差异,各柜组所需营业员人数是不同的。营业员人数过少,顾客等待时间就长,会影响服务质量;营业员人数过多,则会造成人力资源的浪费,影响劳动效率。在已经测得平均额流量和平均服务时间的条件下,如何科学合理地确定营业员人数,并核定营业员的工作量和劳动报酬,便成为当前商业零售企业管理中迫切需要解决的问题。
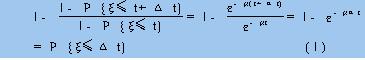
对于客流量,“潜在”的顾客数远远大于已到来的顾客数,不管已接待了多少个顾客,“潜在”的顾客数几乎总量不变,顾客的到来与服务情况无关。
因此,当已知时刻t系统所处状态i(即已知N(t)=i),则在时刻t+△t(△t>0)时系统状态与时刻t之前的任一时刻系统状态无关,所以{N(t),t≥0}是一个马尔可夫过程,实际上,它是齐次可数的。
现设时刻t正在接受服务的顾客为k(k≤m),那么由(1)式,在(t,t+△t)内恰有s个顾客结束服务的概率为:

至于客流量,有如下分析:

以Pij表示系统状态由i变为j的条件转移概率,即Pij=P{N(t+△t)=j|N(t)=i}
Pi为无条件概率,即 Pi=P{N(t)=i},由于
{系统状态不变}={没有顾客结束服务,也没有顾客到来}∪{恰有一个顾客结束服务,恰有一个顾客到来}∪{有两个或两个以上的顾客结束服务,有相同数量的顾客到来}
上式第3个事件的概率,根据(3)、(6)式,应为o(△t),因此,由(3),(4),(5)式可得到
P{系统状态不变}=Pii(△t)
=[1—iμ△t+o(△t)][1—λ△t+o(△t)]+[iμ△t+o(△t)]
[λ△t+o(△t)]+o(△t)
=1—(iμ+λ)△t+o(△t)(7—1)(i≤m)
当i>m,则有Pij(△t)=1(mμ+λ)△t+o(△t)(7—2)
类似地,容易得到


营业员人数m根据下列原则确定:
(1)根据有关规定,一柜组当班营业员至少要有2人;
(2)λ/mμ>1;
(3)应有较大的概率使任意时刻到来的顾客立即得到服务或仅等待一个短时间后可得到服务。
根据对合肥市银河大厦百货商场三个不同柜组的实测结果,设定当班营业员人数为2,2,3时,根据公式(11),(12),(14),计算得到的数据见附表。
当N(t)<m时,在时刻t到来的顾客不需等待立即可得到服务,当N(t)=i≥m时,在时刻t到来的顾客必须等待,此时,等待时间小于△t的概率较难得到,但必定有
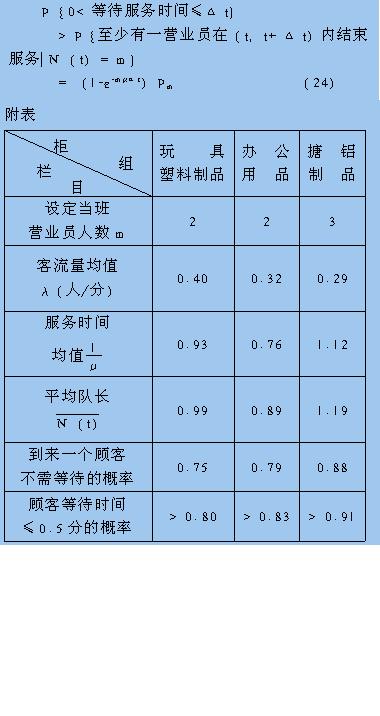
(表中所列概率,是在每个营业员每次只能接待一个顾客的假定下得到,根据实际观察,当服务时间超过2分钟时,营业员有可能可以同时接待另一个顾客,所以,实际上顾客不需或只需等待一个短时间的概率要稍大些。)
根据上表可以得出如下结论:
1、严格控制商品质量,执行商品上柜前的检验制度,能有效地缩短服务时间,减少服务人员。
2、除节假日外,平均的客流量较小,这说明合肥市外来客流量较小,柜组现在的人员编制数都超过附表中设定的人数,因此,提高服务质量,在人员数量上不存在制约因素,今后随着经济的发展,客流量增加的情况下,现有人员也是足够的。
3、比较各柜组在销售中的工作量,以λ/μ为标准较合理,衡量人均工作量,则以λ/(mμ)(m为每班营业员编制数)较好,由于客流量大小及商品价格相差悬殊(从几角至数百元甚至数千元,相差数千至上万倍),销售额在经营不同商品的柜组之间没有可比性,但可作为同一柜组不同期间的工作量比较标准,结合λ/(mμ)的测算和销售额可以在不同柜组中制订比较合理的按劳计酬方法
华东经济管理 张乃峰 常宗耀 |