|
社会消费品零售总额反映了经济运行中的一个重要环节———消费,为了更好地了解和把握市场消费动态,要求对该指标进行月度预测。本文以广州市的社会消费品零售总额指标为例,计算该指标的月度预测模型
市场经济中,政府对市场变化的即时反应是各国经济工作的重点。在我国,随着市场经济的日益成熟,各级政府逐渐认识到短期计划的重要性。在要求减少对市场干预的同时,政府在经济中的作用主要体现在保证经济运行的正常轨道。因此,强调了政府的短期调整,也就适应了市场变化的灵敏度。过去我国一直强调长期计划,统计信息机构中均缺乏短期经济指标,如季度、月度指标,同时,对短期预测也还未形成统一模式。
本文以广州市的社会消费品零售总额指标为例,计算该指标的月度预测模型。社会消费品零售总额反映了经济运行中的一个重要环节———消费。在我国改革开放以来,消费领域出现过几次大的动荡,每一次都对社会生产造成很大影响。尤其是目前我国市场上的消费需求不足现象,使我国经济发展受到外需与内需两方的困扰。传统的年度指标已不能满足经济部门工作的需要,从1994年起,广州市开始统计月度社会消费品零售总额。为了更好地了解和把握市场消费动态,要求对该指标进行月度预测。
一、模型拟合
从1994年至1998年,该指标的统计只有短短5年时间。由于数据资料不足的限制,很难运用常见的ARIMA时间序列模型进行拟合预测。笔者尝试以一般回归方法对数据进行分析处理,得到了较理想的拟合效果(数据见下表)。
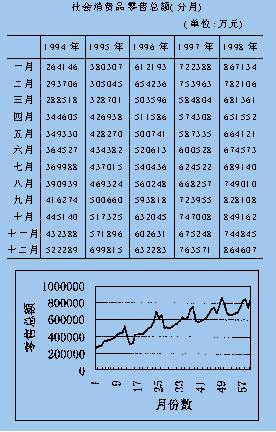
根据表中数据,得到右图。可以看到,各年零售额存在明显的季节性,每年年末,零售额有明显的增长,即翘尾影响;每年的三、四月份,零售额为全年的最低水平。另外,曲线随时间呈明显的线性上升趋势。
本文采用统计软件SAS进行拟合。以月零售总额为因变量;以两个虚拟变量分别反映两种方向不同的季节影响;以时间为因变量解释上升趋势;另外,为了取得更好的拟合效果,设模型为一阶滞后。得到如下方程:
SALE=169248+4012. 8T+62886D1-72338D2+0. 4879SALE(T-1)
t值 5. 324 4. 577 3 .542 -3. 266 4.958
p值 0. 0001 0. 0001 0. 0008 0. 0019 0. 0001
R square=0 9178 adjR square=0 9117
F=150 786 DW=1 773
其中,SALE———月度社会消费零售总额;T———时间(以1994年1月为1);
SALE(T 1)———月度社会消费总额的一阶滞后;
D1=1,当每年12月或者1月;否则,D1=0
D2=1,当每年3月;否则,D2=0;
模型的拟合效果见下图:
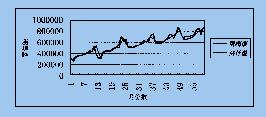
从以上结果可见,模型的拟合效果较好。所设的4个因变量能解释自变量变动的91 78%;此外,由DW∈(DU,4 DU)=(1 444,1 727)可推知,模型不存在一阶自相关。
二、预测
拟合模型的建立主要目的在于预测,但由于资料数据不足,本模型不适合进行长期预测,否则将会出现较大误差。以下,是本文运用该模型对广州市的社会消费品零售总额进行1年内(1999年)的预测结果:
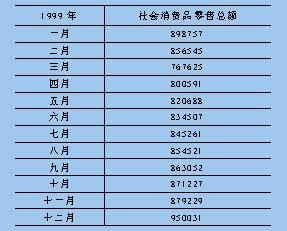
统计教育 袁婕 |