您现在的位置： 新语文 >> 市场营销 >> 营销攻略 >> 营销战略 >> 正文
[组图]竞争企业产品开发的博奕分析           ★★★ 【字体：小 大】
竞争企业产品开发的博奕分析

作者：佚名     人气：394    全球最全的财富中文资源平台

本文应用博奕论的思想和方法，分析在竞争市场条件下，竞争企业的产品开发策略，包括企业获得先行优势的条件，以及先行优势与竞争企业间相对生产成本的关系。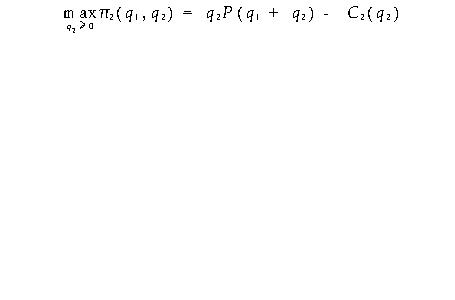
　　一、 引　言
　　博奕论（ｇａｍｅｔｈｅｏｒｙ），又称对策论，是研究决策主体的行为发生直接相互作用时的决策以及这种决策的均衡问题的科学。１９９４年诺贝尔经济学奖授予了美国的纳什（Ｎａｓｈ）教授和海萨尼（ｈａｒｓａｎｙｉ）、德国的泽尔腾（Ｓｅｌｔｅｎ）教授三位博奕论专家，１９９６年又有在博奕论的应用方面（税收激励机制、信息经济学）作出卓越贡献的两位大师获此殊荣。从８０年代开始，博奕论逐渐成为主流经济学的一部分，甚至可以说成为微观经济学的基础，“事实上，它（博奕论）几乎吞没了整个微观经济学，就如同计量经济学吞没了‘经验经济学’（ｅｍｐｉｒｉｃａｌ　ｅｃｏｎｏｍｉｃｓ）一样”（ＥｒｉｃＲａｓｍｕｓｅｎ，１９８９年）。同时，现代市场竞争，发展到白热化程度和高峰时期，竞争主体相互之间的策略产生直接影响，竞争更加明确化和公开化，这种竞争又常常是在有限个直接的竞争对手之间展开的。这正好反映了现代市场竞争更趋明确化、直接化、激烈化、集中化以及高层次化的特点，而现代博奕论正好作为研究竞争问题的最有力和最有效的工具之一。
　　本文拟采用博奕论的思想和方法，研究竞争企业间的产品开发及其决策问题，其中包括开发新产品的有利条件、策略选择等问题。
　　二、 模　型
　　我们考虑这样的问题：在竞争市场条件下，当市场需求存在时，企业希望能通过开发生产新产品，首先占领市场，以获得更多利润。然而企业在制定新产品开发和生产策略的过程中，常常要面对极大的开发费用，如产品研制费用、技术设备更新或添加费用，以及市场开发费用等。而尾随他人仿制的费用，相形之下，可说是微不足道的。显然，企业在选择“开发新产品”和“等待别人新产品出现后跟进仿制”时，如果不存在先行优势，它将倾向于后者。那么，在什么条件下企业有着先开发新产品的积极性呢？也就是企业在什么情况下才能获得先行优势呢？企业的先行优势与其自身的生产成本和竞争对手的生产成本有着怎样的关系？
　　下面我们以两寡头卖方垄断竞争来展开对问题的讨论。
　　假设有两个参与人，分别称为企业１和企业２；每个企业的策略是选择产量；支付是利润，它是两个企业产量的函数；参与人的行动顺序为，企业１（称为领头企业，ｌｅａｄｅｒ）首先选择产量ｑ１≥０，企业２（称为尾随企业，ｆｏｌｌｏｗｅｒ）观测到ｑ１，然后选择自己的产量ｑ２≥０。
　　为分析方便，用ｑｉ∈Ｑｉ＝［０，＋∞］表示企业ｉ的产量，Ｃｉ（ｑｉ）表示成本函数，Ｐ＝Ｐ（ｑ１＋ｑ２）表示逆需求函数（其中，Ｐ是价格，Ｑ（Ｐ）是需求函数）。另假设，企业１为获取先行地位，比如首先开发新产品，要付出更高的代价，即使生产成本增加ΔＣｉ（ｑｉ），比如产品的开发费、市场开发费等。
　　显然，这是一个完美信息动态博奕。
　　由上述假设我们可以得出企业的利润函数分别是：
　　领先企业１的利润函数为：
　　∏１（ｑ１，ｑ２）＝ｑ１Ｐ（ｑ１＋ｑ２）－（Ｃ１（ｑ１）＋ΔＣ（ｑ１））　　
　　尾随企业２的利润函数为：
　　　　∏２（ｑ１，ｑ２）＝ｑ２Ｐ（ｑ１＋ｑ２）－Ｃ２（ｑ２）　　
　　因为企业２在选择ｑ２前观测到企业１的选择ｑ１，它可以根据ｑ１来选择ｑ２，而企业１首先行动，它不可能根据ｑ２来选择ｑ１，因此，企业２的策略应是从Ｑ１到Ｑ２的函数，
即　　　　　　Ｓ２：Ｑ１→Ｑ２
　　而企业１的策略就是简单地选择ｑ１。
　　对这一博奕问题的求解应使用子博奕精炼纳什均衡概念，即应用逆向归纳法。
　　首先考虑在给定ｑ１的条件下，企业２的最优选择，企业２在第二阶段的问题是：


　　该问题的最优化一阶条件是：

　　其中，Ｑ＝ｑ１＋ｑ２
　　解方程式（１）可得：
　　　　ｑ２＝Ｓ２（ｑ１）
　　由于企业１预期到企业２将根据Ｓ２（ｑ１）选择ｑ２，因此，企业１在第一阶段的问题是：

　　该问题的最优化一阶条件是：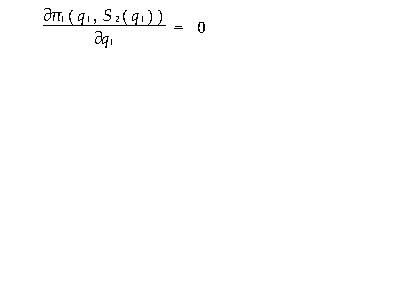

即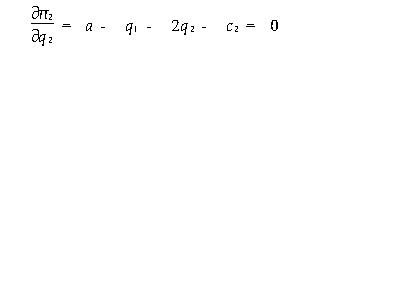

　　解方程（２）即可求得ｑ１，即企业１的最优选择，再将ｑ１代入Ｓ２（ｑ１）即可求出企业２的最优选择ｑ２。
　　于是，我们得到该完美信息动态博奕的子博奕精炼纳什均衡（ｑ１，Ｓ１（ｑ１））。
　　为了得出具体的结果以方便分析，我们考虑上述模型的一简化形式。假设企业具有不变的单位成本ｃｉ，
　　即　　Ｃｉ（ｑ１）＝ｃｉｑｉ　　　　ｉ＝１，２
　　逆需求函数为一线性函数Ｐ（Ｑ）＝ａ－ｑ１－ｑ２，其中ａ为大于零的常数。
　　又假设企业１获得先行地位，使单位成本增加Δｃ，那么，支付（利润）函数分别为：
　　企业１：　∏１（ｑ１，ｑ２）＝ｑ１（Ｐ（Ｑ）－ｃ１－Δｃ）　　（３）
　　企业２：　∏２（ｑ１，ｑ２）＝ｑ２（Ｐ（Ｑ）－ｃ２）　　　　　（４）
　　由最优化一阶条件式（１），式（２）可得：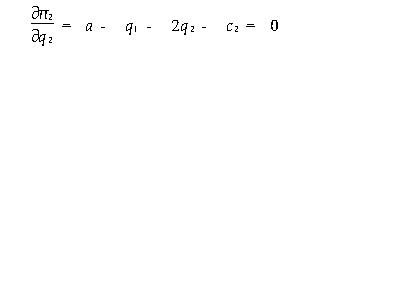

　　解得：　　ｑ２＝Ｓ２（ｑ１）＝１／２（ａ－ｑ１－ｃ２）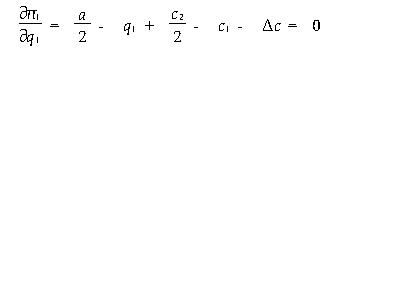

解得：　　　ｑ１＝１／２ａ＋ｃ２－２（ｃ１＋Δｃ）　　　　 　　　（５）
代（５）式入Ｓ２（ｑ１），得：
　　　　　ｑ２＝Ｓ２（ｑ１）＝１／４ａ－３ｃ２＋２（ｃ１＋Δｃ）　（６）
此处假设ａ＞ｍａｘ｛２（ｃ１＋Δｃ）－ｃ２，３ｃ２－２（ｃ１＋Δｃ）｝　　
　　将式（５），式（６）分别代入式（３），式（４）可得均衡时企业的利润为：

　　要使企业１有首先开发新产品的激励，即企业１必须具有先行优势，即∏１＞∏２。
计算易得知，仅当下述条件成立时，企业１才具有先行优势，

［ｐｉｃ８．ｊｐｇ］
即Δｃ的右端限制值Ａ关于企业１的单位成本ｃ１单调递减，而关于企业２的单位成本ｃ２单调递增，这说明，企业的生产成本越低，它越愿意开发新产品，以取得先行优势。又由式（７）得：
［ｐｉｃ９．ｊｐｇ］
　　三、分　析
　　由上述两式可知，先行企业在均衡时的利润关于其单位成本单调递减，而关于尾随企业的单位成本单调递增，这进一步说明在竞争企业间，当具有先行优势时，相对成本越低，企业先行优势越大，也就是说，先行更有利可图。这正好解释了在现实竞争中，在新产品开发方面，开发费用极大，而仿制费用相对较小时，为什么仍然不断有新产品问世，其重要原因就是先行优势的存在，而新产品，特别是技术水平要求较高的产品（常伴随更高的生产成本）常常由技术水平较高的企业首先推出。
因此，由上述分析，我们可以得出如下的结论，在竞争市场条件下，企业希望通过开发新产品，以获取更大利润，必须以自身的技术水平的提高，单位成本的降低为基础。只有技术领先，劳动生产率高，从而相对（单位）生产成本较低的企业才有可能通过先行而获得更大利益，即具有先行优势。这也从另一方面说明了，在现代市场条件下，企业提高管理水平，加强技术改造，增加技术投入以提高劳动生产率，降低生产成本在市场竞争中对企业生存和发展的重要性。
财富论今——新的理念  心的飞越   
  • 上一篇财富：

  • 下一篇财富：
    •  财富论今－http://cf.xinyuwen.com   苏ICP备05013302号
    打造全球最全最实用的财富中文资源平台！     新的理念   心的飞越