教学目标：

　　1、使学生进一步理解二次函数的基本性质；

　　2、渗透解析几何，数形结合，函数等数学思想.培养学生发现问题解决问题，及逻辑思维的能力.

　　3、使学生参与教学过程，通过主体的积极思维，体验感悟数学.逐步建立数学的观念，培养学生独立地获取知识的能力.

　　教学重点：初步理解数形结合的数学思想

　　教学难点：初步理解数形结合的数学思想

　　教学用具：微机

　　教学方法：探究式、小组合作学习

　　教学过程：

　　例1、已知：抛物线y=x²－（m²－1）x－2m²－2

　　⑴求证：无论m取什么实数，抛物线与x轴一定有两个交点

　　⑵m取什么实数时，两交点间距离最短？是多少？

　　解：

　　　△ = (m²－1)²＋4(2m²＋2)

　　　= m⁴－2m²＋1＋8m²＋8

　　　= m⁴＋6m²＋9

　　　= (m²＋3)²

　　　m²≥0

　　　∴m²＋3＞0

　　　∴△＞0 

　　　∴抛物线与x轴有两个交点

　　问题：为什么说当△＞0时，抛物线y = ax²+bx+c与x轴有两个交点.（能否从数和形两方面说明）

　　设计意图：在课堂上创设让学生说数学的机会，学会合作学习，以达到①经验共享，在思维的碰撞中共同提高.②学会合作，消除个人中心.③发现自我，提高参与度.④弘扬个体的主体性，形成健康，丰富的个性.

　　数：点在曲线上，点的坐标满足曲线的方程.反之，曲线方程的每一个实数解对应的点都在曲线上.抛物线与x轴的交点，既在抛物线上，又在x轴上.所以交点的坐标既满足抛物线的解析式，也满足x轴的解析式.设交点坐标为（x，y）

　　∴

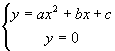
　　    这样交点问题就转化成求这个二元二次方程组的解.代入y = 0，消去y，转化成ax²+bx+c=0这个一元二次方程求根问题.根据以前学过的知识，当△＞0时， ax²+bx+c=0有两个不相等的实根.∴y = ax²+bx+c

　　y = 0

　　有两个不等的实数解

　　∴抛物线与ｘ轴交于两个不同的点.

　　形：顶点在ｘ轴上方，且开口向下.或者顶点在ｘ轴下方，且开口向上.

　　设计意图：渗透解析几何的基本思想

　　使学生掌握转化思想使学生在解题过程中，感知数学的直观性和形式化这二重性.掌握数形结合，分类讨论的思想方法.逐步学会数学的思维.

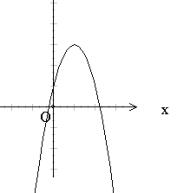
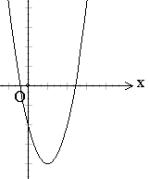
　　转化成代数语言为：

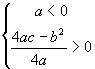
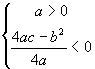
　　小结：第一种方法，根据解析几何的基本思想.将求曲线的交点问题，转化成求方程组的解的问题.

　　第二种方法，借助于图象思考问题，比较直观.发现规律后，再用数学的符号语言将其形式化.这既体现了数学中的数形结合的思想方法，也是探索解数学问题的一般方法.

　　思考：试从数、形两方面说明抛物线与x轴的交点个数与判别  式的符号的关系.

　　设计意图：数学学习是一个再创造的过程，不能等同于数学知识的汇集，而要让学生经历数学知识的创造过程.使主体积极地参与到学习中去.以数学知识为载体，揭示出蕴涵于其中的数学思想方法，逐步形成数学观念.

　　⑵m取什么实数时,两交点间距离最短?是多少?

　　解：设二次函数与x轴的两交点为(x₁,0)，(x₂,0)

　　解法㈠ 由⑴可知m为任何实数时, 都有△＞0

　　解①

　　　∴  x₁＋x₂=m²－1

　　　x_1·x₂=－2(m²＋1)

　　　∴│x₂－x₁│=

　　　=

　　　=

　　　=

　　　= m²＋3

　　　∴当m =0时,两交点最小距离为3

　　这里两交点间距离是m的函数

　　设计意图：培养学生的问题意识.在解题过程中，发现问题，并能运用已有的数学知识，将其一般化，形式化，解决问题，体会数学问题解决的一般方法.培养学生独立地获取数学知识的能力.渗透函数思想

此文章共有2页  第 1 2 页