 打印本文
打印本文  关闭窗口
关闭窗口
一、教学目标
1.理解成比例线段以及项、比例外项、比例内项、第四比例项、比例中项等的概念.
2.掌握比例基本性质和合分比性质.
3.通过通过的应用,培养学习的计算能力.
4.通过比例性质的教学,渗透转化思想.
5.通过比例性质的教学,激发学生学习兴趣.
二、教学设计
先学后做,启发引导
三、重点及难点
1.教学重点 比例性质及应用.
2.教学难点 正确理解成比例线段及应用.
四、课时安排
1课时
五、教具学具准备
股影仪、胶片、常用画图工具
六、教学步骤
【复习提问】
1.什么是线段的比?
2.已知![]() 这两条线段的比是
这两条线段的比是![]() 吗,为什么?
吗,为什么?
【讲解新课】
1.比例线段:见教材P203页。
如:见教材P203页图5-2。
又如:![]()
![]() 即a、b、c、d是成比例线段。
即a、b、c、d是成比例线段。
注:①已知![]() 问这四条线段成比例吗?
问这四条线段成比例吗?
(答:成比例。![]() ,这里与顺序无关)。
,这里与顺序无关)。
②若已知a、b、c、d是成比例线段,是指![]() 不能写成
不能写成![]() (在说四条线段成比例时,一定要将这四条线段按顺序列出,这里与顺序有关)。
(在说四条线段成比例时,一定要将这四条线段按顺序列出,这里与顺序有关)。
板书教材P203页比例线段的一些附属概念。
2.比例的性质:
(1)比例的基本性质:如果![]() ,那么
,那么![]() 。
。
它的逆命题也成立,即:如果![]() ,那么
,那么![]() 。
。
推论:如果![]() ,那么
,那么![]() 。
。
反之亦然:如果![]() ,那么
,那么![]() 。
。
①基本性质证明了“比例式”和“等积式”是可以互化的。
②由![]() ,除可得到
,除可得到![]() 外,还可得到其它七个比例式。即由一个等积式
外,还可得到其它七个比例式。即由一个等积式![]() ,可写成八个不同的比例式(让学生试写)。然后教师教给方法。即:先按左:右=右:左“写出四个比例式。
,可写成八个不同的比例式(让学生试写)。然后教师教给方法。即:先按左:右=右:左“写出四个比例式。![]() 。再由等式的对称性写出另外四个比例式:
。再由等式的对称性写出另外四个比例式:![]() 。注意区别与联系。
。注意区别与联系。
③用比例的基本性质,可检查所作的比例变形是否正确。即把比例式化成等积式,看与原式所得的等积式是否相同即可。
④等积化比例、比例化等积是本章一个重要能力,要使学生达到非常熟练的程度,以利于后面学习。
(2)合比性质:如果![]() ,那么
,那么![]()
证明:∵![]() ,∴
,∴![]() 即:
即:![]()
同理可证:![]() (找学生板演)
(找学生板演)
(3)等比性质:如果![]()
那么![]()
证明:设![]() ;则
;则![]()
∴![]()
等比性质的证明思路及思想非常重要,它是解决数学中连比问题的通法,希望同学们认真体会,务必掌握。
例1(要求了解即可)
(1)已知:![]() ,求证:
,求证:![]() 。
。
证明:∵![]() ,∴
,∴![]()
“通法”:∵![]() ,∴
,∴![]() 即
即![]()
(2)已知:![]() ,求证:
,求证:![]() 。
。
方法一:![]()
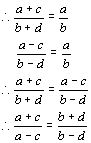
方法二:![]()
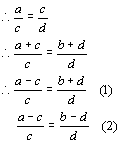
(1)÷(2)得:![]()
【小结】
(1)比例线段的概念及附属概念。
(2)比例的基本性质及其应用。
八、布置作业
(1)求![]()
①![]() ②
②![]() ③
③![]()
(2)求下列各式中的x
①![]() ②
②![]() ③
③![]() ④
④![]()
九、板书设计
|
比例线段(二) 1.比例线段: 教师板书定义 ……… 比例线段的附属概念 ……… |
2.比例的性质 (1)比例基本性质 ………… 注意:(1) ② ③ |
3.课堂练习 |
 打印本文
打印本文  关闭窗口
关闭窗口