第一课时 圆周角（一）

　　教学目标：

　　（1）理解圆周角的概念,掌握圆周角的两个特征、定理的内容及简单应用；

　　（2）继续培养学生观察、分析、想象、归纳和逻辑推理的能力；

　　（3）渗透由“特殊到一般”，由“一般到特殊”的数学思想方法．

　　教学重点：圆周角的概念和圆周角定理

　　教学难点：圆周角定理的证明中由“一般到特殊”的数学思想方法和完全归纳法的数学思想．

　　教学活动设计：（在教师指导下完成）

　　（一）圆周角的概念

　　1、复习提问：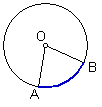

　　（1）什么是圆心角？

　　答：顶点在圆心的角叫圆心角.

　　（2）圆心角的度数定理是什么？

　　答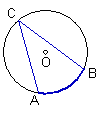：圆心角的度数等于它所对弧的度数.（如右图）

　　2、引题圆周角：

　　如果顶点不在圆心而在圆上，则得到如左图的新的角∠ACB，它就是圆周角.（如右图）（演示图形，提出圆周角的定义）

　　定义：顶点在圆周上，并且两边都和圆相交的角叫做圆周角

　　3、概念辨析：

　　教材P93中1题：判断下列各图形中的是不是圆周角，并说明理由．

　　学生归纳：一个角是圆周角的条件：①顶点在圆上；②两边都和圆相交.

　　（二）圆周角的定理

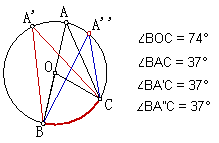
　　1、提出圆周角的度数问题

　　问题：圆周角的度数与什么有关系？

　　经过电脑演示图形，让学生观察图形、分析圆周角与圆心角，猜想它们有无关系．引导学生在建立关系时注意弧所对的圆周角的三种情况：圆心在圆周角的一边上、圆心在圆周角内部、圆心在圆周角外部．

　　（在教师引导下完成）

　　（1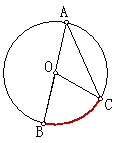）当圆心在圆周角的一边上时，圆周角与相应的圆心角的关系：（演示图形）观察得知圆心在圆周角上时，圆周角是圆心角的一半.

　　提出必须用严格的数学方法去证明.

　　证明:(圆心在圆周角上)

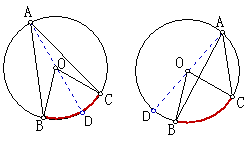　　 （2）其它情况，圆周角与相应圆心角的关系：

　　当圆心在圆周角外部时（或在圆周角内部时）引导学生作辅助线将问题转化成圆心在圆周角一边上的情况，从而运用前面的结论，得出这时圆周角仍然等于相应的圆心角的结论.

　　证明：作出过C的直径（略）

　　圆周角定理: 一条弧所对的

　　周角等于它所对圆心角的一半.

　　说明：这个定理的证明我们分成三种情况.这体现了数学中的分类方法；在证明中，后两种都化成了第一种情况，这体现数学中的化归思想.（对A层学生渗透完全归纳法）

　　（三）定理的应用

　　1、例题: 如图   OA、OB、OC都是圆O的半径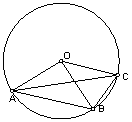， ∠AOB=2∠BOC．

　　求证：∠ACB=2∠BAC

　　让学生自主分析、解得，教师规范推理过程．

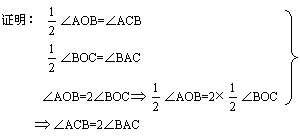
　　说明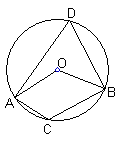：①推理要严密；②符号“”应用要严格，教师要讲清．

　　2、巩固练习:

　　（1）如图，已知圆心角∠AOB=100°，求圆周角∠ACB、∠ADB的度数？

　　（2）一条弦分圆为1：4两部分，求这弦所对的圆周角的度数？

　　说明：一条弧所对的圆周角有无数多个，却这条弧所对的圆周角的度数只有一个，但一条弦所对的圆周角的度数只有两个．

　　（四）总结

　　知识：（1）圆周角定义及其两个特征；（2）圆周角定理的内容．

　　思想方法：一种方法和一种思想：

　　在证明中，运用了数学中的分类方法和“化归”思想．分类时应作到不重不漏；化归思想是将复杂的问题转化成一系列的简单问题或已证问题．

　　（五）作业 教材P100中 习题A组6,7,8

此文章共有2页  第 1 2 页