[教学目标]

1．会说出边角边。

2．会运用边角边证明两个三角形全等的简单问题，并能正确地写出证明过程。

[引导性材料]

画一个三角形，使它和课本第2页图3－1中的△ABC全等，你准备怎么画？

（教学中多数学生根据定义用透明纸或较薄的纸描一个三角形以及用复写纸复印一个三角形。设计画三角形的活动，实质是营造新问题的背景。）

[教学设计]

问题1：每个同学用一张纸，如图3．5－l剪一个三角形，你有没有办法使全班同学剪下的三角形是全等三角形？

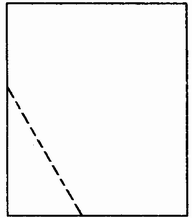
图3．5－1

问题2：从上面剪全等的直角三角形中，可以发现，有一个直角以及两条直角边对应相等的两个直角三角形全等。类似地，量得课本第2页图3－l中，∠B＝40°，AB＝3．1cm，BC＝3cm有这三个条件，你猜想可以画出一个三角形与课本第2页图3－1中的△ABC全等吗？

问题3：根据上述三个条件画三角形，你认为可以按怎样顺序画图？

读句画图：

（l）画∠DBE＝40°

（2）在BD、BE上分别截取BA＝3．1cm，BC=3cm。

（3）连结AC、得△ABC。

把你所画的△ABC剪下来，放到课本第2页图3－1上，观察这两个三角形是否全等？

从上面的实验可以发现，两个三角形有两边和它们的夹角对应相等，这两个三角形全等。我们把这个事实作为判定两个三角形全等的条件──边角边。可以简写成“边角边”或“SAS”。

练一练：课本例1后练习第1题。

说明：1．问题l借助学生已有的生活经验，让学生主动发现“有一个直角及两条直角边对应相等的两个三角形全等”。并通过问题2引导学生从特殊到一般的研究中主动获取知识。

2．本设计针对几何入门阶级，学生几何语言学习中难以把画图过程表述为规范的文字语言，先让学生用通俗的语言作铺垫，然后安排读句画图的活动，从而体现规范化的几何语言，严谨、简练、准确的概括几何事实的特殊功能。引导学生逐步熟悉常用的重要几何术语。

[例题解析]

例：（即课本例1）

　[课堂练习]

（补充练习）1．用两个全等三角形透明塑料片拼出图3．5－2、3、4后，变换其中一个三角形的位置，使两个三角形重合。

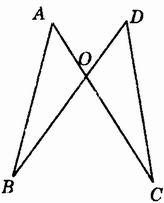
图3．5－2

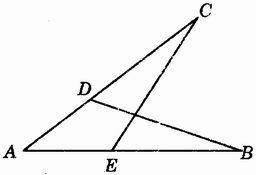
图3．5－3

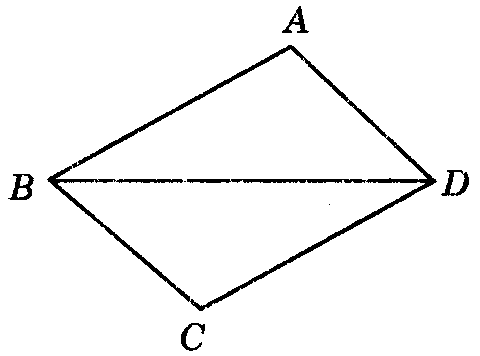
图3．5－4

2．在下列推理中填写需要补充的条件，使结论成立：

（1）如图3．5－2，在△AOB和△DOC中。

AO＝DO（已知）,

____=_____(),

BO=CO(已知)，

∴△AOB≌△DOC（）。

（2）如图3．5－3，在△AEC和△ADB中，

____=_____（已知）,

∠A＝∠A(公共角),

____=_____（已知）,

∴△AEC≌△ADB（）。

（3）如图3．5－4，在△ABD和△DCB中，

　AD＝CB（已知）,

____=_____(已知),

BD=____()，

∴△ABD≌△CDB（SAS）。

说明：1．补充练习1安排拼图和图形变换的活动，逐步提高学生的识图能力和培养学生动态研究几何图形的意识。

2．补充练习2，使学生在例1的基础上进一步熟悉推理论证的模式，熟悉推证三角形全等中常用的直接条件（对顶角、公共边、公共角），使大多数学生能顺利地跨度，正式进入演绎推理的第一步。

[小结]

1．应用边角边判定两个三角形全等，要按照它的条件，准确地找出“对应相等”的边和角，此如图3．5－5，△ABC和△DEF中，虽然AB＝DF，∠B＝∠E，BC＝DF，但是相等的边和角不具有相同的顺序，不难看出，这两个三角形不全等。可见，有两边和一角相等的两个三角形不一定全等。

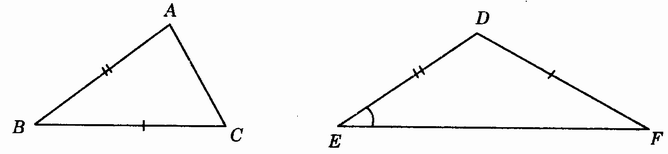
图3．5－5

2．寻找使结论成立所需条件，要注意充分利用图形中的隐含条件，如公共边、公共角、对顶角等。

[作业]

1．课本例1后练习第2题。

2．课本习题3．2A组第5、6、7题。