 打印本文
打印本文  关闭窗口
关闭窗口 教学目标
1.使学生理解最简二次根式的概念;
2.掌握把二次根式化为最简二次根式的方法.
教学重点和难点
重点:化二次根式为最简二次根式的方法.
难点:最简二次根式概念的理解.
教学过程设计
一、导入新课
计算:
![]()
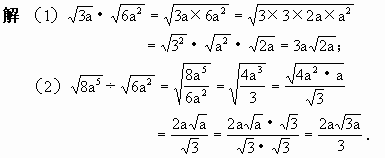
我们再看下面的问题:
![]()
![]() 简,得到
简,得到
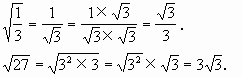
![]()
从上面例子可以看出,如果把二次根式先进行化简,会对解决问题带来方便.
二、新课![]()
答:
1.被开方数的因数是整数或整式;
2.被开方数中不含能开得尽方的因数或因式.
满足上面两个条件的二次根式叫做最简二次根式.
例1 试判断下列各式中哪些是最简二次根式,哪些不是?为什么?
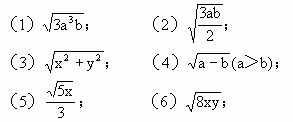
解 (l)不是最简二次根式.因为a3=a2·a,而a2可以开方,即被开方数中有开得尽方的因式.
![]() 整数.
整数.
(3)是最简二次根式.因为被开方数的因式x2+y2开不尽方,而且是整式.
(4)是最简二次根式.因为被开方数的因式a-b开不尽方,而且是整式.
(5)是最简二次根式.因为被开方数的因式5x开不尽方,而且是整式.
(6)不是最简二次根式.因为被开方数中的因数8=22·2,含有开得尽的因数22.
指出:从(1),(2),(6)题可以看到如下两个结论.
1.在二次根式的被开方数中,只要含有分数或小数,就不是最简二次根式;
2.在二次根式的被开方数中的每一个因式(或因数),如果幂的指数等于或大于2,也不是最简二次根式.
例2 把下列各式化为最简二次根式:
![]()
分析:把被开方数分解因式或因数,再利用积的算术平方根的性质![]()
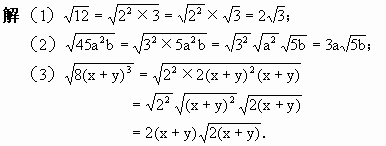
例3 把下列各式化成最简二次根式:
![]()
分析:题(l)的被开方数是带分数,应把它变成假分数,然后将分母有理化,把原式化成最简二次根式.
题(2)及题(3)的被开方数是分式,先应用商的算术平方根的性质把原式表示为两个根式的商的形式,再把分母有理化,把原式化成最简二次根式.
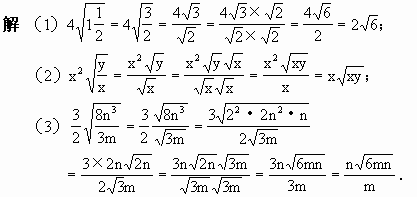
通过例2、例3,请同学们总结出把二次根式化成最简二次根式的方法.
答:如果被开方数是分式或分数(包括小数)先利用商的算术平方根的性质,把它写成分式的形式,然后利用分母有理化化简.
如果被开方数是整式或整数,先把它分解因式或分解因数,然后把开得尽方的因式或因数开出来,从而将式子化简.
三、课堂练习
1.在下列各式中,是最简二次根式的式子为 [ ]
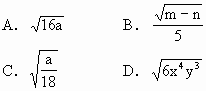
![]()
的二次根式的式子有_____个. [ ]
A.2 B.3
C.1 D.0
3.把下列各式化成最简二次根式:
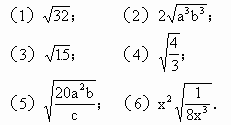
答案:
1.B
2.B

四、小结
1.最简二次根式必须满足两个条件:
(1)被开方数的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式.
2.把一个式子化为最简二次根式的方法是:
(1)如果被开方数是整式或整数,先把它分解成因式(或因数)的积的形式,把开得尽方的因式(或因数)移到根号外;
(2)如果被开方数含有分母,应去掉分母的根号.
五、作业
1.把下列各式化成最简二次根式:
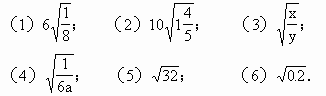
2.把下列各式化成最简二次根式:
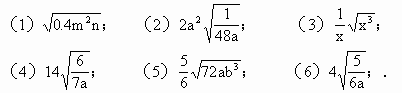
答案:

 打印本文
打印本文  关闭窗口
关闭窗口