教学目标

　　（1）掌握“两个正数的算术平均数不小于它们的几何平均数”这一重要定理；
　　（2）能运用定理证明不等式及求一些函数的最值；
　　（3）能够解决一些简单的实际问题；
　　（4）通过对不等式的结构的分析及特征的把握掌握重要不等式的联系；
　　（5）通过对重要不等式的证明和等号成立的条件的分析，培养学生严谨科学的认识习惯，进一步渗透变量和常量的哲学观；

教学建议

1．教材分析

（1）知识结构

　　本节根据不等式的性质推导出一个重要的不等式： ，根据这个结论，又得到了一个定理： ，并指出了 为 的算术平均数， 为 的几何平均数后，随后给出了这个定理的几何解释。

（2）重点、难点分析

　　本节课的重点内容是掌握“两个正数的算术平均数不小于它们的几何平均数”；掌握两个正数的和为定值时积有最大值，积为定值时和有最小值的结论，教学难点是正确理解和使用平均值定理求某些函数的最值．为突破重难点，教师单方面强调是远远不够的，只有让学生通过自己的思考、尝试，注意到平均值定理中等号成立的条件，发现使用定理求最值的三个条件“一正，二定，三相等”缺一不可，才能大大加深学生对正确使用定理的理解，教学中要注意培养学生分析归纳问题的能力，帮助学生形成知识体系，全面深刻地掌握平均值定理求最值和解决实际问题的方法．

㈠定理教学的注意事项

　　在公式 以及算术平均数与几何平均数的定理的教学中，要让学生注意以下两点：

　　（1） 和 成立的条件是不同的：前者只要求 都是实数，而后者要求 都是正数。

　　例如 成立，而 不成立。

　　（2）这两个公式都是带有等号的不等式，因此对其中的“当且仅当……时取‘=’号”这句话的含义要搞清楚。教学时，要提醒学生从以下两个方面来理解这句话的含义：

　　当 时取等号，其含义就是：

　　仅当 时取等号，其含义就是：

　　综合起来，其含义就是： 是 的充要条件。

（二）关于用定理证明不等式

　　当用公式 ， 证明不等式时，应该使学生认识到：

　　它们本身也是根据不等式的意义、性质或用比较法（将在下一小节学习）证出的。因此，凡是用它们可以获证的不等式，一般也可以直接根据不等式的意义、性质或用比较法证明。

（三）应用定理求最值的条件

　　应用定理时注意以下几个条件：

　　（1）两个变量必须是正变量；

　　（2）当它们的和为定值时，其积取得最大值；当它们的积是定值时，其和取得最小值；

　　（3）当且仅当两个数相等时取最值．

　　即必须同时满足“正数”、“定值”、“相等”三个条件，才能求得最值．

　　在求某些函数的最值时，还要注意进行恰当的恒等变形、分析变量、配置系数．

（四）应用定理解决实际问题的分析

　　在应用两个正数的算术平均数与几何平均数的定理解决这类实际问题时，要让学生注意；

　　（1）先理解题意，设变量，设变量时一般把要求最大值或最小值的变量定为函数；

　　（2）建立相应的函数关系式，把实际问题抽象为函数的最大值或最小值问题；

　　（3）在定义域内，求出函数的最大值或最小值；

　　（4）正确写出答案。

2．教法建议

　　（1）导入新课建议采用学生比较熟悉的问题为背景，这样容易被学生接受，产生兴趣，激发学习动机．使得学生学习本节课知识自然且合理．
　　（2）在新授知识过程中，教师应力求引导、启发，让学生逐步回忆所学的知识，并应用它们来分析问题、解决问题，以形成比较系统和完整的知识结构．对有关概念使学生理解准确，尽量以多种形式反映知识结构，使学生在比较中得到深刻理解．
　　（3）教学方法建议采用启发引导，讲练结合的授课方式，发挥教师主导作用，体现学生主体地位，学生获取知识必须通过学生自己一系列思维活动完成，启发诱导学生深入思考问题，有利于培养学生思维灵活、严谨、深刻等良好思维品质．
　　（4）可以设计解法的正误讨论，这样能够使学生尝试失败，并从失败中找到错误原因，加深对正确解法的理解，真正把新知识纳入到原有认知结构中．
　　（5）注意培养应用意识．教学中应不失时机地使学生认识到数学源于客观世界并反作用干客观世界．为增强学生的应用意识，在平时教学中就应适当增加解答应用问题的教学，使学生不禁感到“数学有用，要用数学”．

教学目标：

　　1．学会推导并掌握两个正数的算术平均数与几何平均数定理；
　　2．理解定理的几何意义；
　　3．能够简单应用定理证明不等式.

教学重点：均值定理证明

教学难点：等号成立条件

教学方法：引导式

教学过程：

一、复习回顾

　　上一节，我们完成了对不等式性质的学习，首先我们来作一下回顾.

（学生回答）

　　由上述性质，我们可以推导出下列重要的不等式.

二、讲授新课

1．  重要不等式：

　　如果

　　证明：

　　当

　　所以，

　　即

　　由上面的结论，我们又可得到

2．  定理：如果 是正数，那么

　　证明：∵

　　即

　　显然，当且仅当

　　说明：ⅰ）我们称 的算术平均数，称 的几何平均数，因而，此定理又可叙述为：两个正数的算术平均数不小于它们的几何平均数.

　　ⅱ） 成立的条件是不同的：前者只要求 都是实数，而后者要求 都是正数.

　　ⅲ）“当且仅当”的含义是充要条件.

3．均值定理的几何意义是“半径不小于半弦”.

　　以长为 的线段为直径作圆，在直径AB上取点C， .过点C作垂直于直径AB的弦DD′,那么

　　即

　　这个圆的半径为 ，显然，它不小于CD，即 ，其中当且仅当点C与圆心重合；即 时，等号成立.

在定理证明之后，我们来看一下它的具体应用.

4．  例题讲解：

　　例1 已知 都是正数，求证：

　　（1）如果积 是定值P,那么当 时，和 有最小值

　　（2）如果和 是定值S,那么当 时，积 有最大值 证明：因为 都是正数，所以

　　（1）积xy为定值P时，有

　　上式当 时，取“=”号，因此，当 时，和 有最小值 .

　　（2）和 为定值S时，有

　　上式当 时取“=”号，因此，当 时，积 有最大值 .

　　说明：此例题反映的是利用均值定理求最值的方法，但应注意三个条件：

　　（1）函数式中各项必须都是正数;

　　（2）函数式中含变数的各项的和或积必须是常数；

　　（3）等号成立条件必须存在.

　　接下来，我们通过练习来进一步熟悉均值定理的应用.

三、课堂练习

　　课本P₁₁练习2，3

　　要求：学生板演，老师讲评.

课堂小结：

　　通过本节学习，要求大家掌握两个正数的算术平均数不小于它们的几何平均数的定理，并会应用它证明一些不等式，但是在应用时，应注意定理的适用条件.

课后作业：习题6.2   1，2，3，4

板书设计：

第二课时

教学目标：

　　1．进一步掌握均值不等式定理；
　　2．会应用此定理求某些函数的最值；
　　3．能够解决一些简单的实际问题.

教学重点：均值不等式定理的应用

教学难点：

　　解题中的转化技巧

教学方法：启发式

教学过程：

一、复习回顾

　　上一节，我们一起学习了两个正数的算术平均数与几何平均数的定理，首先我们来回顾一下定理内容及其适用条件.

（学生回答）

　　利用这一定理，可以证明一些不等式，也可求解某些函数的最值，这一节，我们来继续这方面的训练.

二、讲授新课

　　例2 已知都是正数，求证：

　　分析：此题要求学生注意与均值不等式定理的“形”上发生联系，从而正确运用，同时加强对均值不等式定理的条件的认识.

　　证明：由 都是正数，得

　　即

　　例3  某工厂要建造一个长方体无盖贮水池，其容积为 ，深为3m，如果池底每 的造价为150元，池壁每 的造价为120元，问怎样设计水池能使总造价最低，最低总造价是多少元？

　　分析：此题首先需要由实际问题向数学问题转化，即建立函数关系式，然后求函数的最值，其中用到了均值不等式定理.

　　解：设水池底面一边的长度为xm，水池的总造价为l元，根据题意，得

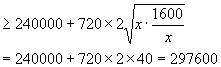
　　当

　　因此，当水池的底面是边长为40m的正方形时，水池的总造价最低，最低总造价是297600元.

　　评述：此题既是不等式性质在实际中的应用，应注意数学语言的应用即函数解析式的建立，又是不等式性质在求最值中的应用，应注意不等式性质的适用条件.

　　为了进一步熟悉均值不等式定理在证明不等式与求函数最值中的应用，我们来进行课堂练习.

三、课堂练习

　　课本P₁₁练习1，4

要    求：学生板演，老师讲评.

课堂小结：

　　通过本节学习，要求大家进一步掌握利用均值不等式定理证明不等式及求函数的最值，并认识到它在实际问题中的应用.

课后作业：

　　习题6.2    5,6,7

板书设计：

均值不等式                  例2 §6.2.2      例3         学生 定理回顾                    ……           …… ……                        ……           ……         练习 ……                        ……           ……