 打印本文
打印本文  关闭窗口
关闭窗口 教学目标
(1)掌握绝对值不等式的基本性质,在学会一般不等式的证明的基础上,学会含有绝对值符号的不等式的证明方法;
(2)通过含有绝对值符号的不等式的证明,进一步巩固不等式的证明中的由因导果、执要溯因等数学思想方法;
(3)通过证明方法的探求,培养学生勤于思考,全面思考方法;
(4)通过含有绝对值符号的不等式的证明,可培养学生辩证思维的方法和能力,以及严谨的治学精神。
教学建议
一、知识结构
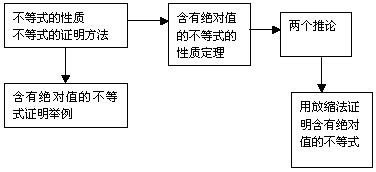
二、重点、难点分析
① 本节重点是性质定理及推论的证明.一个定理、公式的运用固然重要,但更重要的是要充分挖掘吸收定理公式推导过程中所蕴含的数学思想与方法,通过证明过程的探求,使学生理清思考脉络,培养学生勤于动脑、勇于探索的精神.
② 教学难点一是性质定理的推导与运用;一是证明含有绝对值的不等式的方法选择.在推导定理中进行的恒等变换与不等变换,相对学生的思维水平是有一定难度的;证明含有绝对值的不等式的方法不外是比较法、分析法、综合法以及简单的放缩变换,根据要证明的不等式选择适当的证明方法是无疑学生学习上的难点.
三、教学建议
(1)本节内容分为两课时,第一课时为含有绝对值的不等式性质定理的证明及简单运用,第二课时为含有绝对值的不等式的证明举例.
(2)课前复习应充分.建议复习:当 ![]() 时
时
![]() ;
;
![]() ;
;
以及绝对值的性质:
![]() ,为证明例1做准备.
,为证明例1做准备.
(3)可先不给出含有绝对值的不等式性质定理,提出问题让学生研究: ![]() 是否等于
是否等于 ![]() ?大小关系如何?
?大小关系如何? ![]() 是否等于
是否等于 ![]() ?等等.提示学生用一些数代入计算、比较,以便归纳猜想一般结论.
?等等.提示学生用一些数代入计算、比较,以便归纳猜想一般结论.
(4)不等式 ![]() 的证明方法较多,也应放手让学生去探讨.
的证明方法较多,也应放手让学生去探讨.
(5)用向量加减法的三角形法则记忆不等式及推论 ![]() .
.
(6)本节教学既要突出教师的主导作用,又要强调学生的主体作用,课上尽量让全体学生参与讨论,由基础较差的学生提出猜想,由基础较好的学生帮助证明,培养学生的团结协作的团队精神.
教学设计示例
含有绝对值的不等式
教学目标
理解 ![]() 及其两个推论,并能应用它证明简单含有绝对值不等式的证明问题。
及其两个推论,并能应用它证明简单含有绝对值不等式的证明问题。
教学重点难点
重点是理解掌握定理及等号成立的条件,绝对值不等式的证明。
难点是定理的推导过程的探索,摆脱绝对值的符号,通过定理或放缩不等式。
教学过程
一、复习引入
我们在初中学过绝对值的有关概念,请一位同学说说绝对值的定义。
当 ![]() 时,则有:
时,则有: 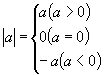
那么 ![]() 与
与 ![]() 及
及 ![]() 的大小关系怎样?
的大小关系怎样?
这需要讨论 当 ![]()
当 ![]()
当 ![]()
综上可知: ![]()
我们已学过积商绝对值的性质,哪位同学回答一下?
![]() .
.
当 ![]() 时,有:
时,有: ![]() 或
或 ![]() .
.
二、引入新课
由上可知,积的绝对值等于绝对值的积;商的绝对值等于绝对值的商。
那么和差的绝对值等于绝对值的和差吗?
1.定理探索
和差的绝对值不一定等于绝对值的和差,我们猜想
![]() .
.
怎么证明你的结论呢?
用分析法,要证 ![]() .
.
只要证 ![]()
即证 ![]()
即证 ![]() ,
,
而 ![]() 显然成立,
显然成立,
故 ![]()
那么怎么证 ![]() ?
?
同样可用分析法
当 ![]() 时,显然成立,
时,显然成立,
当 ![]() 时,要证
时,要证 ![]()
只要证 ![]() ,
,
即证 ![]()
而 ![]() 显然成立。
显然成立。
从而证得 ![]() .
.
还有别的证法吗?(学生讨论,教师提示)
由 ![]() 与
与 ![]() 得
得 ![]() .
.
当我们把 ![]() 看作一个整体时,上式逆用
看作一个整体时,上式逆用 ![]() 可得什么结论?
可得什么结论?
![]() 。
。
能用已学过得的 ![]() 证明
证明 ![]() 吗?
吗?
可以 ![]() 表示为
表示为 ![]()
![]() .
.
即 ![]() (教师有计划地板书学生分析证明的过程)
(教师有计划地板书学生分析证明的过程)
就是含有绝对值不等式的重要定理,即 ![]() .
.
由于定理中对 ![]() 两个实数的绝对值,那么三个实数和的绝对值呢?
两个实数的绝对值,那么三个实数和的绝对值呢? ![]() 个实数和的绝对值呢?
个实数和的绝对值呢?
亦成立 ![]()
![]()
![]()
这就是定理的一个推论,由于定理中对 ![]() 没有特殊要求,如果用
没有特殊要求,如果用 ![]() 代换
代换 ![]() 会有什么结果?(请一名学生到黑板演)
会有什么结果?(请一名学生到黑板演)
![]() ,
,
用 ![]() 代
代 ![]() 得
得 ![]() ,
,
即 ![]() 。
。
这就是定理的推论 ![]() 成立的充要条件是什么?
成立的充要条件是什么?
![]()
那么 ![]() 成立的充要条件是什么?
成立的充要条件是什么?
![]() .
.
例1 已知 ![]() ,求证
,求证 ![]() . (由学生自行完成,请学生板演)
. (由学生自行完成,请学生板演)
证明: ![]()
![]()
![]()
![]()
![]()
例2 已知 ![]() ,求证
,求证 ![]() .
.
证明: ![]()
![]()
点评:这是为今后学习极限证明做准备,要习惯和“配凑”的方法。
例3 求证 ![]() .
.
证法一:(直接利用性质定理)在 ![]() 时,显然成立.
时,显然成立.
当 ![]() 时,左边
时,左边 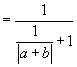
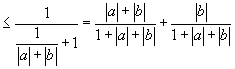
![]() .
.
证法二:(利用函数的单调性)研究函数 ![]() 在
在 ![]() 时的单调性。
时的单调性。
设 ![]() ,
,
![]() ,
, ![]() 在
在 ![]() 时是递增的.
时是递增的.
又 ![]() ,将
,将 ![]() ,
, ![]() 分别作为
分别作为 ![]() 和
和 ![]() ,则有
,则有
![]() (下略)
(下略)
证法三:(分析法)原不等式等价于![]() ,
,
只需证 ![]() ,
,
即证 ![]()
又 ![]() ,
,
![]() 显然成立.
显然成立.
![]() 原不等式获证。
原不等式获证。
还可以用分析法证得 ![]() ,然后利用放缩法证得结果。
,然后利用放缩法证得结果。
三、随堂练习
1.①已知 ![]() ,求证
,求证 ![]() .
.
②已知 ![]() 求证
求证 ![]() .
.
2.已知 ![]() 求证:
求证:
① ![]() ;
;
② ![]() .
.
3.求证 ![]() .
.
答案:1. 2. 略
3. ![]() 与
与 ![]() 同号
同号 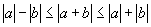
四、小结
1.定理 ![]() . 把
. 把 ![]() 、
、 ![]() 、
、 ![]() 看作是三角形三边,很象三角形两边之和大于第三边,两边之差小于第三边,这样理解便于记忆,此定理在后面学习复数时,可以推广到比较复数的模长,并有其几何意义,有时也称其为“三角形不等式”.
看作是三角形三边,很象三角形两边之和大于第三边,两边之差小于第三边,这样理解便于记忆,此定理在后面学习复数时,可以推广到比较复数的模长,并有其几何意义,有时也称其为“三角形不等式”.
2.平方法能把绝对值不等式转化为不含绝对值符号的不等式,但应注意两边非负时才可平方,有些证明并不容易去掉绝对值符号,需用定理 ![]() 及其推论。
及其推论。
3.对 ![]() 要特别重视.
要特别重视.
五、布置作业
1.若 ![]() ,则不列不等式一定成立的是( )
,则不列不等式一定成立的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
2.设 ![]() 为满足
为满足 ![]() 的实数,那么( )
的实数,那么( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
3.能使不等式 ![]() 成立的正整数
成立的正整数 ![]() 的值是__________.
的值是__________.
4.求证:
(1) ![]() ;
;
(2) ![]() .
.
5.已知 ![]() ,求证
,求证 ![]() .
.
答案:1. D 2. B 3.1、2、3
4. ![]()
![]()
5. 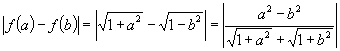
= ![]()
注:也可用分析法.
六、板书设计
|
6.5含有绝对值的不等式(一) | ||
|
1.复习 2.定理 推论 |
例1 例2 |
例3 课堂训练 |
 打印本文
打印本文  关闭窗口
关闭窗口