打印本文 
关闭窗口 教学目标
1.掌握等比数列前 项和公式，并能运用公式解决简单的问题.
（1）理解公式的推导过程，体会转化的思想；
（2）用方程的思想认识等比数列前 项和公式，利用公式知三求一；与通项公式结合知三求二；
2.通过公式的灵活运用，进一步渗透方程的思想、分类讨论的思想、等价转化的思想.
3.通过公式推导的教学，对学生进行思维的严谨性的训练，培养他们实事求是的科学态度.
教学建议
教材分析
（1）知识结构
先用错位相减法推出等比数列前 
项和公式，而后运用公式解决一些问题，并将通项公式与前 
项和公式结合解决问题，还要用错位相减法求一些数列的前 
项和.
（2）重点、难点分析
教学重点、难点是等比数列前 
项和公式的推导与应用.公式的推导中蕴含了丰富的数学思想、方法（如分类讨论思想，错位相减法等），这些思想方法在其他数列求和问题中多有涉及，所以对等比数列前 
项和公式的要求，不单是要记住公式，更重要的是掌握推导公式的方法. 等比数列前 
项和公式是分情况讨论的，在运用中要特别注意 
和 
两种情况.
教学建议
（1）本节内容分为两课时，一节为等比数列前 
项和公式的推导与应用，一节为通项公式与前 
项和公式的综合运用，另外应补充一节数列求和问题.
（2）等比数列前 
项和公式的推导是重点内容，引导学生观察实例，发现规律，归纳总结，证明结论.
（3）等比数列前 
项和公式的推导的其他方法可以给出，提高学生学习的兴趣.
（4）编拟例题时要全面，不要忽略 
的情况.
（5）通项公式与前 
项和公式的综合运用涉及五个量，已知其中三个量可求另两个量，但解指数方程难度大.
（6）补充可以化为等差数列、等比数列的数列求和问题.
教学设计示例
课题：等比数列前 
项和的公式
教学目标
（1）通过教学使学生掌握等比数列前 
项和公式的推导过程，并能初步运用这一方法求一些数列的前 
项和.
（2）通过公式的推导过程，培养学生猜想、分析、综合能力，提高学生的数学素质.
（3）通过教学进一步渗透从特殊到一般，再从一般到特殊的辩证观点，培养学生严谨的学习态度.
教学重点，难点
教学重点是公式的推导及运用，难点是公式推导的思路.
教学用具
幻灯片，课件，电脑.
教学方法
引导发现法.
教学过程
一、新课引入：
（问题见教材第129页）提出问题： 
（幻灯片）
二、新课讲解：
记 
，式中有64项，后项与前项的比为公比2，当每一项都乘以2后，中间有62项是对应相等的，作差可以相互抵消.
（板书）即 
， ①
， ②
②－①得 
即 .
由此对于一般的等比数列，其前 
项和 
，如何化简？
（板书）等比数列前 
项和公式
仿照公比为2的等比数列求和方法，等式两边应同乘以等比数列的公比 
，即
（板书） 
③两端同乘以 
，得
④，
③－④得 
⑤，（提问学生如何处理，适时提醒学生注意 
的取值）
当 
时，由③可得 
（不必导出④，但当时设想不到）
当 
时，由⑤得 
.
于是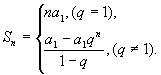 
反思推导求和公式的方法——错位相减法，可以求形如 
的数列的和，其中 
为等差数列， 
为等比数列.
（板书）例题：求和： 
.
设 
，其中 
为等差数列， 
为等比数列，公比为 
，利用错位相减法求和.
解： 
，
两端同乘以 
，得
，
两式相减得 
于是 
.
说明：错位相减法实际上是把一个数列求和问题转化为等比数列求和的问题.
公式其它应用问题注意对公比的分类讨论即可.
三、小结：
1.等比数列前 
项和公式推导中蕴含的思想方法以及公式的应用；
2.用错位相减法求一些数列的前 
项和.
四、作业：略.
五、板书设计：
|
等比数列前 |
打印本文 关闭窗口