教学建议

　　1、教材分析

　　（1）知识结构

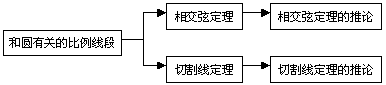
　　（2）重点、难点分析

　　重点：相交弦定理及其推论，切割线定理和割线定理．这些定理和推论不但是本节的重点、本章的重点，而且还是中考试题的热点；这些定理和推论是重要的工具性知识，主要应用与圆有关的计算和证明．

　　难点：正确地写出定理中的等积式．因为图形中的线段较多，学生容易混淆．

　　2、教学建议

　　本节内容需要三个课时．第1课时介绍相交弦定理及其推论，做例1和例2．第2课时介绍切割线定理及其推论，做例3．第3课时是习题课，讲例4并做有关的练3．

　　（1）教师通过教学，组织学生自主观察、发现问题、分析解决问题，逐步培养学生研究性学习意识，激发学生的学习热情；

　　（2）在教学中，引导学生“观察——猜想——证明——应用”等学习，教师组织下，以学生为主体开展教学活动．

第1课时：相交弦定理

　　教学目标：

　　1．理解相交弦定理及其推论，并初步会运用它们进行有关的简单证明和计算；

　　2．学会作两条已知线段的比例中项；

　　3．通过让学生自己发现问题，调动学生的思维积极性，培养学生发现问题的能力和探索精神；

　　4．通过推论的推导，向学生渗透由一般到特殊的思想方法．

　　教学重点：

　　正确理解相交弦定理及其推论．

　　教学难点：

　　在定理的叙述和应用时，学生往往将半径、直径跟定理中的线段搞混，从而导致证明中发生错误，因此务必使学生清楚定理的提出和证明过程，了解是哪两个三角形相似，从而就可以用对应边成比例的结论直接写出定理．

　　教学活动设计

　　（一）设置学习情境

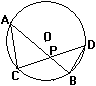　　 1、图形变换：（利用电脑使AB与CD弦变动）

　　①引导学生观察图形，发现规律：∠A＝∠D，∠C＝∠B．

　　②进一步得出：△APC∽△DPB．

　　 ．

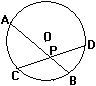　　 ③如果将图形做些变换，去掉AC和BD，图中线段 PA，PB，PC，PO之间的关系会发生变化吗?为什么?

　　组织学生观察，并回答．

　　2、证明：

　　已知：弦AB和CD交于⊙O内一点P．

　　求证：PA·PB＝PC·PD．

　　（A层学生要训练学生写出已知、求证、证明；B、C层学生在老师引导下完成）

　　（证明略）

　　（二）定理及推论

　　1、相交弦定理： 圆内的两条相交弦，被交点分成的两条线段长的积相等．

　　结合图形让学生用数学语言表达相交弦定理：在⊙O中；弦AB，CD相交于点P，那么PA·PB＝PC·PD．

　　2、从一般到特殊，发现结论．

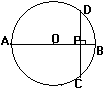　　 对两条相交弦的位置进行适当的调整，使其中一条是直径，并且它们互 相垂直如图，AB是直径，并且AB⊥CD于P．

　　提问：根据相交弦定理，能得到什么结论?

　　指出：PC²＝PA·PB．

　　请学生用文字语言将这一结论叙述出来，如果叙述不完全、不准确．教师纠正，并板书．

　　推论 如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项．

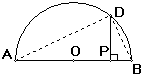　　 3、深刻理解推论：由于圆是轴对称图形，上述结论又可叙述为：半圆上一点C向直径AB作垂线，垂足是P，则PC²＝PA·PB． 

　　若再连结AC，BC，则在图中又出现了射影定理的基本图形，于是有：

　　PC²＝PA·PB ；AC²＝AP·AB；CB²＝BP·AB

　　（三）应用、反思

　　例1 已知圆中两条弦相交，第一条弦被交点分为12厘米和16厘米两段，第二条弦的长为32厘米，求第二条弦被交点分成的两段的长．

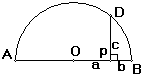　　 引导学生根据题意列出方程并求出相应的解．

　　例2  已知：线段a，b．

　　求作：线段c，使c²＝ab．

　　分析：这个作图求作的形式符合相交弦定理的推论的形式，因此可引导学生作出以线段a十b为直径的半圆，仿照推论即可作出要求作的线段．

　　作法：口述作法．

　　反思：这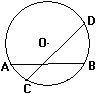个作图是作两已知线段的比例中项的问题，可以当作基本作图加以应用．同时可启发学生考虑通过其它途径完成作图．

　　练习1 如图，AP＝2厘米，PB＝2．5厘米，CP＝1厘米，求CD．

　　变式练习：若AP＝2厘米，PB＝2．5厘米，CP，DP的长度皆为整数．那么CD的长度是 多少?

　　 将条件隐化，增加难度，提高学生学习兴趣

　　练习2 如图，CD是⊙O的直径，AB⊥CD，垂足为P，AP＝4厘米，PD＝2厘米．求PO的长．

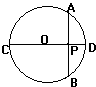
　　练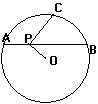习3  如图：在⊙O中，P是弦AB上一点，OP⊥PC，PC 交⊙O于C．  求证：PC²＝PA·PB 

　　引导学生分析：由AP·PB，联想到相交弦定理，于是想到延长 CP交⊙O于D，于是有PC·PD＝PA·PB．又根据条件OP⊥PC．易 证得PC＝PD问题得证．

　　（四）小结

　　知识：相交弦定理及其推论；

　　能力：作图能力、发现问题的能力和解决问题的能力；

　　思想方法：学习了由一般到特殊(由定理直接得到推论的过程)的思想方法．

　　（五）作业

　　教材P132中 9，10；P134中B组4(1)．

此文章共有2页  第 1 2 页