教学设计示例1

　　教学目标：

　　（1）了解用量角器等分圆心角来等分圆；掌握用尺规作圆内接正方形和正六边形，能作圆内接正八边形、正三角形、正十二边形；

　　（2）通过画图培养学生的画图能力；

　　（3）对学生进行审美教育，提高学生的审美能力，促进学生对几何学习的热情．

　　教学重点：

　　(1)量角器等分圆心角来等分圆；

　　(2)尺规作圆内接正方形和正六边形．

　　教学难点：

　　准确作图．

　　教学活动设计：

　　（一）提出问题：

　　由于正多边形在生产、生活实际中有广泛的应用性，所以会画正多边形应是学生必备能力之一．

　　问题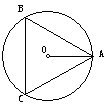1：已知⊙O的半径为2cm，求作圆的内接正三角形．

　　教师组织学生进行，方法不限．

　　目的：充分发展学生的发散思维．

　　（二）解决问题：

　　以下为解决问题的参考方案：(上课时教师归纳学生的方法)

　　(1)度量法：①用量角器或30°角的三角板度量，使∠BAO=∠CAO=30°．

　　②用量角器度量，使∠AOB=∠BOC=∠COA=120°．

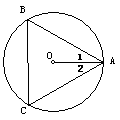
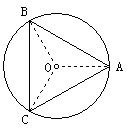
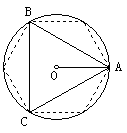
　　(2)尺规法：（如上右图）用圆规在⊙O上截取长度等于半径（2cm）的弦，连结AB、BC、CA即可．

　　(3)计算与尺规结合法：由正三角形的半径与边长的关系可得，正三角形的边长= R=2（cm），用圆规在⊙O上截取长度为2（cm）的弦AB、AC，连结AB、BC、CA即可．

　　（三）研究、归纳

　　1、用量角器等分圆：

　　依据：等圆中相等的圆心角所对应的弧相等．

　　操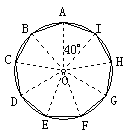作：两种情况：其一是依次画出相等的圆心角来等分圆，这种方法比较准确，但是麻烦；其二是先用量角器画一个圆心角，然后在圆上依次截取等于该圆心角所对弧的等弧，于是得到圆的等分点，这种方法比较方便，但画图的误差积累到最后一个等分点，使画出的正多边形的边长误差较大．

　　问题2：把半径为2cm⊙O九等份．

　　（先画半径2cm的圆，然后把360°的圆心角9等份，每一份40°）

　　归纳：用量角器等分圆，方法简便，可以把圆任意n等分，但有误差．

　　2、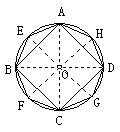用尺规等分圆：

　　（1）问题3：作正四边形、正八边形．

　　教师组织学生，分析、作图．

　　归纳：只要作出已知⊙O的互相垂直的直径即得圆内接正方形，再过圆心作各边的垂线与⊙O相交，或作各中心角的角平分线与⊙O相交，即得圆接正八边形，照此方法依次可作正十六边形、正三十二边形、正六十四边形……

　　（2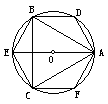）问题4：作正六、三、十二边形．

　　教师组织学生，分析、作图．

　　归纳：先作出正六边形，则可作正三角形，正十二边形，正二十四边形………理论上我们可以一直画下去，但大家不难发现，随着边数的增加，正多边形越来越接近于圆，正多边形将越来越难画．

　　（四）总结

　　（1）用量角器等分圆周作正n边形；

　　（2）用尺规作正方形及由此扩展作正八边形、用尺规作正六边形及由此扩展作正12边形、正三角形．

　　（五）作业 教材P173中13．

此文章共有2页  第 1 2 页