 打印本文
打印本文  关闭窗口
关闭窗口 2004年全国高考湖南卷(理工类)第21题如下:
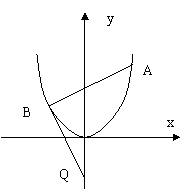
如图,过抛物线x2=4y的对称轴上任一点P(0,m),(m>0)作直线与抛物线交于A、B两点,点Q是点关于原点的对称点。
(1) 设点P分有向线段![]() 所成的比为λ,证明:
所成的比为λ,证明:![]()
经审题,我们不难发现本题已将向量知识融进解析几何题目,给了我们一个重要的启示:伴随着新教材的使用,在解决相关的解析几何题目时,我们可以适时考虑引入向量思想,尤其是在审题时,只要及时捕捉共线与垂直信息,就可利用向量的坐标运算法则处理相关问题。并能在解题过程中体验向量的神奇作用,感悟数学解题过程中的美妙意境。
本题解法:
 设直线方程为y=kx+m带入抛物线方程x2=4y,得
设直线方程为y=kx+m带入抛物线方程x2=4y,得
x-4kx-4m=0 ①
又设A,B两点的坐标分别为(x1,y1),(x2,y2)
P
 由题意可知:P分有向线段
由题意可知:P分有向线段![]() 所成的比为λ。
所成的比为λ。
O
所以:
![]()
易知Q(0,-m),向量
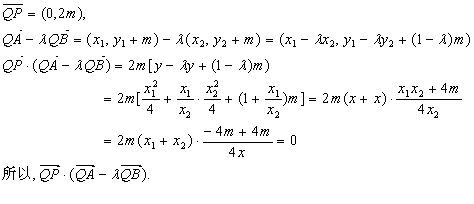
以下枚举几例:
例1.证明点到直线的距离公式:
点P(x0,y0)到直线L:Ax+By+C=0的距离为:![]()
证明:如图(1),作![]()

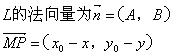
![]()
![]() P
P
因为向量![]() ,所以
,所以![]() M
M
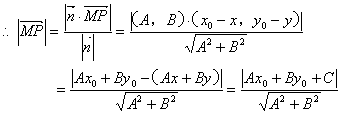 O x
O x
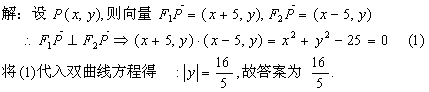

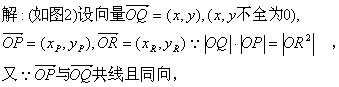
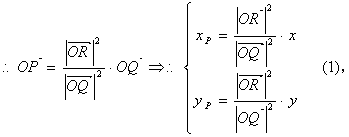


例4.(2000年北京市春季高考试题)设A和B是抛物线y2=4px(p>0)上除原点外的
y
两个动点,已知
![]() 求点M的轨迹方程,并说明轨迹是什么
求点M的轨迹方程,并说明轨迹是什么
A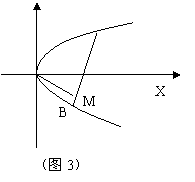
曲线.
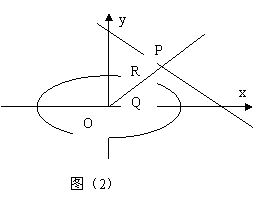
解:(如图3)
O
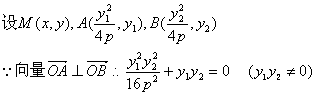
![]()
![]()
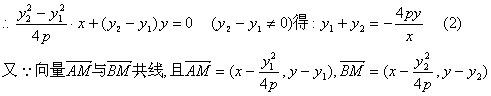
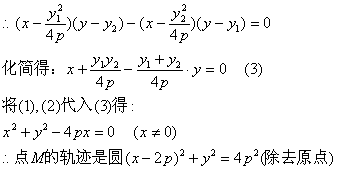
 打印本文
打印本文  关闭窗口
关闭窗口