（二）回归分析(4)　
　　对于使用回归分析需要注意的事项：
　　回归分析方法的普遍性和借助计算机运算的快捷性使得许多研究人员不问该方程与研究现象适合与否或不考虑回归分析的缺陷就盲目使用，其实使用回归分析法是需要许多假设前提的，如果忽略这些前提，就会导出错误甚至是荒谬的结论，这里我们集中讨论一下有关简单回归的缺陷，这些缺陷也同样适用于我们稍后将要提到的多元回归分析。
　　首先，如同在相关分析中看到的，回归分折局限于揭示变量之间的线值关系。如果散点图中所揭示变量之间的规律显著不呈直线变化，那么此时运用回归分析就是非常不适合的（除非通过变量转换变成线性关系）。所以一般只要可能，都要求事先根据数据划出散点图以判断变量之间的联系。
　　其次，通过了显著性检验或佣有较高R2值的回归方程并不一定保证解释变量与被解释变量之间的因果关系，这一点是特别值得注意的；因变量与自变量的设定可能会让粗心的研究者习惯地认为如果回归方程是显著性相关的前者肯定可由后者推导出，但事实上两个变量之间是否有在联系必须从以前的经验和有关的知识理论推导出，而不是由对数据运用的数学方法得出，它只是一个验证。因此谁是因变量，谁是自变量要由研究者自己决定，而不足依赖统计工具。设想有人把经过某一地点各女士裙边离地高度与当时太阳黑子变动的数据合在一起进行分析，如果由此得到的回归方程有0.9的可决系数，是不是就要肯定后者导致了前者的变化呢?这显然是荒谬的。
　　第三,回归方程对于超过给定范围的自变量对应下因变量的预测也就是我们常说的“外推预测”上可信度不高，举一个例子，在研究电视广告与销售额之间关联时电视广告时数变化范围为4～19，对于超过19或低于4的广告时数对应的销售额进行预测时，我们就面临很大的风险。
　　因为我们并不知道当增加新的数据点后散点图是否仍遵循原来的直线。事实上，甚至在原来的范围内，随首X0值对 的偏离，所得到预测的误差都在不断加大(见图9-8)
　　
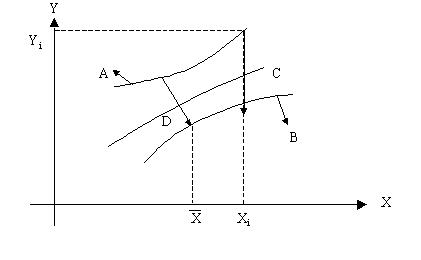
　　图9-8
　　A.B预测值的上下边界
　　C对于点，yi预测值的偏离
　　D最小的预测值的偏离(此时 )
　　第四，建立在小规模样本上的回归方程是不可靠的，极端化而言，仅由两个点推出的简单回归值线方程的可决系数为1，而不论这两点怎样分布，样本的容量进而样本包含的数据点在多元回归中占据着相当重要的地位，在多元回归中如果样本容量不大而又包含太多的自变量的话同样会导致人为形成的高相关度，一般的规则是对于方程中所含的每一个独立变量至少有10个样本数据与之对应。
　　第五，自变量和因变量的数据变化范围能够影响回归方程的可用性，如果要令得出的回归方程具有实用性，自变量和因变量的数据范围就应该宽泛。因为如果有关每个变量的数据过于集中想推出一条准确的直线是非常困难的，对于数据要具有足够离散度这一方面Loefher和luciavish有清晰的论述：
　　很明显，如果因变量没有什么变化，那么没有什么可以需要解释的，因而只需对目标人群的行为做担当少的研究。假定存在一定变动，我们便习探究为什么会这样进而引入自变量来解释。如果这些自变量自身没有任何差异那么它们对于整个问题是没